Метод минимума и максимума

Довольно часто встречаются задачи, в которых требуется определить наибольшее или наименьшее значение величины из всех возможных. Основы такого метода следуют из принципа Ферми, экстремума энергии.

В некоторых задачах удается воспользоваться известными алгебраическими неравенствами (Нер-во Коши).

Задача: Нагруженные сани массой m движутся равномерно по горизонтальной поверхности под действием силы F. Коэффициент трения k. Найти значение минимальной силы и угол между силой и горизонталью.

Из второго закона Ньютона следует: F=

Минимальное значение силы Fmin возможно при максимальном значении знаменателя. Обозначим tg=k.

Заметим, что Sin=; Cos=

Поэтому F=

Максимальное значение =1, откуда

Fmin=

Задача: К висящей очень тонкой пружине жесткостью k подвешен шарик. Вначале пружина не растянута. Затем шарик отпускают. Какой наибольшей скорости достигнет шарик при своем движении? Масса шарика m.

Из закона сохранения энергии

На рис.48 представлен график зависимости . Подставив x=, найдем .

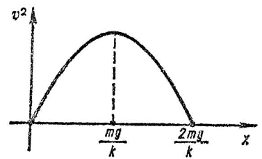
рис.48

Метод софизмов и парадоксов

Метод парадоксов - это создание противоречащих здравому смыслу ситуаций, доказательств, неожиданно и непривычно приводящих к противоречию с традиционными утверждениями и выводами, истинность которых, как кажется не вызывает сомнений. С помощью этого метода понять суть процесса, его тонкости, он стимулирует интерес к учебе.

Софизмы - уловки, выдумки наподобие головоломки, в которых мнимое доказательство выдается за правдоподобное.

Задача: Половину окружности велосипедист на треке проехал с постоянной скоростью . Средняя скорость на всем треке была 10 м/с. Определить скорость на второй половине пути.

Обычно, решение данной задачи получается с помощью известной формулу . Так как , а ,, . В результате получим , подставляя значения получим =-40м/с.

Время движения со средней скоростью должно быть равно сумме времени, затраченного на прохождение каждого участка

или .

Но 2/10=1/5<1/4 …. без прибавления второй дроби.

Значит, что время, затрачиваемое на прохождение первой половины пути, больше, чем время, отпущенное на прохождение с данной средней скоростью всего пути. При таких данных задача лишена смысла.

Задача: В романе "Гектор Сервадак" Жюль Верн описал комету "Галия". Период её обращения вокруг Солнца составил 2 года, а расстояние от Солнца в афелии равнялось 820 млн. км. Могла ли сушествовать такая комета?

Согласно третьему закону Кеплера квадраты периодов небесных тел относятся как кубы больших полуосей их орбит. Зная расстояние от Земли до Солнца (150 млн. км.) и период обращения Земли вокруг него (1 год),

Информация по теме:

Проведение констатирующего эксперимента по изучению сформированности речевых умений детей 2 — 3 летнего возраста
Проведение констатирующего эксперимента, направленного на изучение уровня сформированности речевых умений детей, осуществлялось методом исследования, состоящего из диагностических ситуаций. Блок диагностических ситуаций: «Пассивный взрослый» «Совместная игра со взрослым» «Совместное разглядывание к ...

Особенности речевого развития детей среднего дошкольного возраста
Для успешного решения задач воспитания подрастающего поколения необходимо знание закономерностей физического и психологического развития детей. Становление речи у детей, сущность и закономерности, механизмы этого сложного процесса изучают и представители разных наук - психологи, физиологи, лингвист ...

Система подготовки детей к обучению в школе по программе «Хочу всё знать»
Опытно-экспериментальная работа проводилась на базе ДОУ №24 г. Вольска (воспитатели: В.Ф. Николаева и М.Н. Макарова) с 1 октября 2006 года в подготовительной к школе группе. В группе 19 человек (14 девочек и 5 мальчиков). Опишем систему подготовки детей к школьному обучению в детском саду на базе Д ...