Задачи, решаемые при введении проекционного чертежа

Первой группой таких задач является упражнения, раскрывающие, что неопределенность восстановления оригинала по чертежу устранена на проекционном чертеже. Учитель показывает, что на проекционном чертеже «точка» изображает только точку оригинала, «прямая» - прямую, «плоскость» - плоскость.

На проекционном чертеже становится возможным определять только по изображению взаимное расположение точек, прямых и плоскостей. В порядке упражнения с учащимися рассматриваются способы изображения различных случаев взаимного расположения точки и основной плоскости.

В ходе упражнений учащимся сообщаются и новые необходимые определения.

В этот период следует дать определения «следа» прямой и заданной плоскости. Определения записываются в тетради.

Определение. Следом заданной прямой (плоскости) на основной плоскости называется точка (прямая) пересечения прямой (плоскости) с основной плоскостью.

В итоге обучения решению этих задач учащихся следует познакомить с двумя принципами, на основе которых выполняется построение точек пересечения прямой с плоскостью и построение прямой, по которой пересекаются плоскости.

1) для построения линий пересечения двух плоскостей достаточно знать две точки прямой, по которой пересекаются плоскости, или одну точку и направление прямой. Точки прямой, по которой пересекаются плоскости, определяются как точки пересечения произвольной прямой одной из заданных плоскостей с другой плоскостью.

2) для построения точки пересечения прямой с плоскостью достаточно построить линию пересечения произвольной вспомогательной плоскости, проведенной через данную прямую, с данной плоскостью. Точка пересечения данной прямой с данной плоскостью определяется как точки пересечения данной прямой с линией пересечения вспомогательной и данной плоскостей.

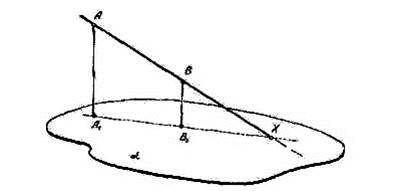Задача: Построить точку пересечения данной прямой АВ (А1В1) с основной плоскостью

Решением этой задачи является точка пересечения (если она существует) прямых АВ и А1В1, так как в оригинале эти прямые лежат в одной и той же проектирующей плоскости.

При определении точек пересечения прямых полезно приучать учащихся с первых же шагов рассматривать построения на проекционном чертеже как проекцию соответственных построений в одной из материальных реализаций оригинала и устанавливать принадлежность или непринадлежность рассматриваемых прямых одной и той же плоскости оригинала. В данном случае, например, построение точки пересечения прямых АВ и А1В1 можно рассматривать как проекцию построений на листе фанеры, представляющим проектирующую плоскость АА1ВВ1.

Задача. Построить (рис.5а) точку пересечения произвольно заданной прямой а(а1) с проектирующей плоскостью φ.

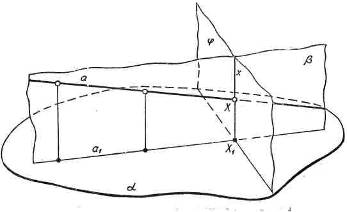
Рис.5а

Для решения задачи проводим через заданную прямую а(а1) вспомогательную проектирующую плоскость и строим линию (х) пересечения вспомогательной и заданной проектирующих плоскостей. Точка Х(Х1) —точка пересечения прямых х и а на изображении— является изображением точки пересечения этих прямых, так как в оригинале эти прямые лежат в одной плоскости. Вместе с тем точка Х(Х1) будет точкой пересечения прямой а(а1) с проектирующей плоскостью φ.

В самом деле, точка Х(Х1) принадлежит прямым а(а1) и х. Прямая х, как линия пересечения плоскостей β и φ, принадлежит плоскости φ. Следовательно, и точка X(X1) принадлежит плоскости φ,т.е. действительно точка X(Х1) является точкой пересечения прямой a(a1) и заданной плоскости.

Информация по теме:

Проблемная лекция и способы организации решения проблемы
Среди форм организации учебного процесса лекции требует более серьезного внимания в разработке способов, приемов активизации познавательной деятельности студентов. В других формах, например, на семинарских лабораторных занятиях, в выполнении курсовых, дипломных работ и других, активизация студентов ...

Клинико-психолого-педагогическая характеристика детей с задержкой психического развития
Понятие "задержка психического развития" (ЗПР) употребляется по отношению к детям со слабо выраженной недостаточностью центральной нервной системы - органической или функциональной. У этих детей нет специфических нарушений слуха, зрения, опорно-двигательного аппарата, тяжелых нарушений ре ...

Понятие «семья»
Семья - это основанное на браке или кровном родстве объединение людей, связанных общностью быта и взаимной ответственностью. Являясь необходимым компонентом социальной структуры любого общества и выполняя множественные социальные функции, семья играет важную роль в общественном развитии. Ф. Энгельс ...