Пересечения треугольника ABC с прямой DE

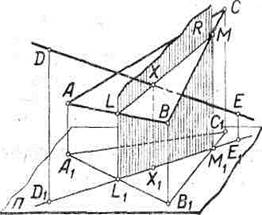
Рис 7б

Находим линию LM пересечения плоскости треугольника ABC с проектирующей плоскостью R, проходящей через данную прямую DE.

В пересечении прямых LМ и DE, лежащих в одной плоскости R, находим искомую точку X, которая на чертеже определяется своим изображением и изображением своей проекции Х1 на плоскость П.

Задача 3. Определить точку пересечения плоскости Q, заданной следом АВ и точкой С, с прямой DE (рис 7в).

Через точку С, принадлежащую плоскости Q, проводим вспомогательную плоскость S, параллельную проектирующей плоскости R, проходящей через данную прямую DE(LC1 || D1E1). Затем находим линию LC пересечения плоскости S с плоскостью Q. Далее строим прямую MX пересечения плоскостей О и R(MX || LC).

Точка X есть искомая точка пересечения, так как она одновременно принадлежит плоскости Q и прямой DE.

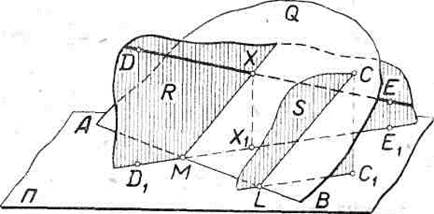
Рис 7в

Решением задачи заканчивается обоснование принципов построения прямых, по которым пересекаются плоскости, и точек пересечения прямых и плоскостей. Однако в классе следует решить еще несколько задач, решение которых сводится к построению точек и линий пересечения прямых и плоскостей.

Итак, при изучении задач на построение на проекционном чертеже учащиеся должны знать, что:

Точку пространства считают заданной на проекционном чертеже, если заданы изображение этой точки и изображение се проекции на основную плоскость.

Прямую считают заданной на проекционном чертеже, если заданы две ее точки или если заданы ее изображение и изображение ее проекции на основную плоскость.

Плоскость считается заданной на проекционном чертеже, если заданы три точки этой плоскости, не лежащие на одной прямой, или прямая и точка вне ее, или две пересекающиеся прямые, или две параллельные прямые.

Если все точки, прямые и плоскости изображенной фигуры являются заданными на проекционном чертеже в указанном смысле, то такое изображение называется полным и можно на нем построением отыскать все непустые пересечения прямых и плоскостей изображенной фигуры, т. е. решать различные позиционные задачи.

Информация по теме:

Творческо-воспроизводящие методы
Ситуационные задачи. Решение ситуационных задач - один из методов активного обучения, направленных на формирование умений и навыков, развитие творческого мышления, приближение к будущей профессиональной деятельности. Основным дидактическим материалом служит ситуационная задача, которая включает в с ...

Нравственное воспитание педагога
Среди требований, предъявляемых к педагогической культуре учителя, есть общечеловеческие, которые были выработаны в ходе развития педагогической практики. Но в сфере педагогического труда свои особенности и влияние имеет и моральная регуляция, неотъемлемым элементом которой является нравственное са ...

Экспериментальная деятельность в детских учреждениях
Цель создания экспериментальной модели "детский сад - начальная школа" была достигнута и в основном исчерпана на организационно - управленческом уровне в связи с утверждением Типового положения (2009) об образовательном учреждении для детей дошкольного и младшего школьного возраста. Педаг ...