Изучение дискретного строения вещества в физике средней школы

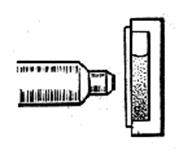
На рисунке показана схема установки Перрена, состоящей из микроскопа с малой глубиной поля зрения и кюветы с эмульсией, а также сильно увеличенный вид этой кюветы сбоку, показывающий распределение броуновских частиц по глубине.

Зная массу одного моля газа и массу одной его молекулы, уже нетрудно сосчитать число молекул в моле:

Повторить опыты Перрена в условиях школьного кабинета физики вряд ли удастся, но можно попытаться хотя бы определить порядок величины числа Авогадро на основе данных уже известного нам простого эксперимента, который мы вполне можем поставить самостоятельно. Это эксперимент с получением тончайшей масляной пленки на поверхности воды.

Если объем капли V, площадь масляного пятна S, толщина слоя d, объем одной молекулы V1, то:

Тогда объем и масса моля вещества:

Отсюда:

В числах это может выглядеть так:

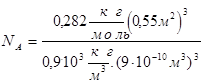
Одно из основных положений молекулярно-кинетической теории гласит, что молекулы находятся в беспрерывном движении. Сражу же возникает вопрос: а каковы скорости движения молекул?

6. Опытное определение скоростей молекул

Впервые прямые измерения скоростей молекул были проведены в 1920 г. немецким физиком О. Штерном.

Идея опыта Штерна состояла в следующем. По оси двух соосных цилиндров, большого и малого, натягивается посеребренная проволока. В малом цилиндре делается узкая щель. Если по проволоке пропускается электрический ток, проволока накаляется, серебро испаряется и его молекулы разлетаются в разные стороны. Молекулы, пролетевшие в щель, оставляют на стенке большого цилиндра след.

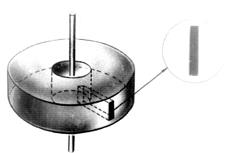
Если цилиндры будут вращаться вокруг общей оси с одинаковой угловой скоростью, то за время, которое необходимо молекулам для того, чтобы пролететь путь L между цилиндрами, внешний цилиндр успеет повернуться на некоторый угол, вследствие чего след от молекулярного пучка сместится на величину S от метки, оставленной им в первом случае. Время поворота внешнего цилиндра относительно внутреннего можно выразить через смещение полоски и линейную скорость вращения v цил . При равномерном вращении, скорость большого цилиндра выражается через его радиус R и период обращения T.

Период же рассчитывается через число оборотов в единицу времени n. Время полета молекул от одного цилиндра до другого выражается через радиусы цилиндров R , r и искомую скорость v мол. Все отмеченные связи представлены ниже двумя способами. В одном случае рассуждения ведутся от искомой величины - скорости газовых молекул. Эта величина связывается с другими величинами. Те, в свою очередь, со следующими. Если величина нам неизвестна, она обводится кружком, если известна или принципиально определяема, то нет.

Во втором случае рассуждения ведутся от основной идеи. В данном случае, это идея о равенстве времен пролета молекулярным пучком расстояния между цилиндрами и поворота цилиндров на некоторый угол, заданный направлениями на две отметки на стенках внешнего цилиндра.

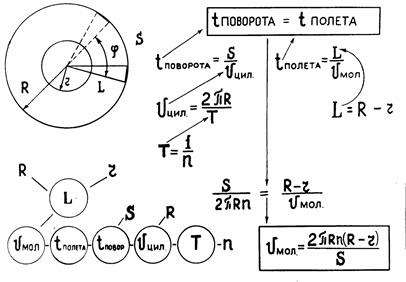
Опыт Штерна дал следующий результат. Смещенная полоска серебра на внешнем цилиндре оказалась размытой, что могло быть объяснено различием скоростей молекул.

Информация по теме:

Рабочая программа производственного обучения
Программа производственного обучения – это документ, определяющий содержание производственного обучения по определенной профессии и специальности, круг умений и навыков, подлежащих усвоению учащимися. Программа производственного обучения разрабатывается на основе Государственного стандарта начально ...

Педагогическое проектирование системы личностно ориентированных дидактических игр
Применение технологий обучения обеспечивает логическую последовательность постановки и решения педагогических задач на основе выбора содержания, форм, методов и средств обучения, адекватного целям подготовки будущего учителя технологии и предпринимательства. Неслучайно поэтому, внедрение педагогиче ...

Способы и правила создания проблемных ситуаций
На основании обобщения передового опыта можно указать несколько основных способов создания проблемных ситуаций. Побуждение учащихся к теоретическому объяснению явлений, фактов, внешнего несоответствия между ними. Это вызывает поисковую деятельность учеников и приводит к активному усвоению новых зна ...