Методы решения физических задач

Метод - это способ познания, исследования явлений.

В широком смысле "метод - это способ действия, осуществление определенно деятельности, достижения какого-либо результата, решения задачи.

Существует много различных методов решения задач по физики, в данном параграфе будут рассмотрены некоторые из методов и примеры решения задач различными способами.

Координатный метод

С помощью этого метода решаются задачи по механики во всех её разделах: кинематике, динамике, статике.

Решение задач кинематики координатным методом.

Основной задачей кинематики является составление уравнений координат тела как функции времени.

В школьном курсе физики это уравнение вида:

Х=Х0+V0хt+ахt2/ 2.

где Х0 - начальная координата материальной точки, V0x - проекция вектора начальной скорости на ось ОХ, аx - проекция вектора ускорения на ось ОХ.

Проекцией вектора на ось - скалярная величина, равная произведению модуля вектора на косинус угла, который этот вектор образует с положительным направлением оси.

В зависимости от угла α проекция вектора может быть положительной при 0о ≤ α < 90о, равной нулю при α = 90о, отрицательной при 90о < α ≤ 180о.

На рис.5 показано определение проекции вектора начальной скорости Voх на ось ОХ, на рис.6 - проекции вектора ускорения ах.

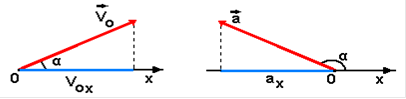
рис.5 рис.6

V0x = V0 cos α; ax = а cos (180o - α) = - a cos α.

Проекция вектора скорости положительна, а проекция вектора ускорения - отрицательна. Знак проекции вектора определяется знаком косинуса угла α. Из уравнения координат тела как функции времени можно получить уравнение для проекции на ось Х вектора скорости как функции времени путём его дифференцирования по времени. Vх=dx/dt=V0х+ ахt. Наиболее общей задачей на движение тела в поле силы тяжести (гравитационном поле) является задача о движении тела, брошенного под углом к горизонту.

Задача: Девочка бросает мяч с балкона, находящегося на высоте h от поверхности земли, под углом α к горизонту со скоростью V0. Определить время полета мяча до земли, дальность полёта (координату Xmax точки падения), наибольшую высоту полёта мяча над землёй (максимальное значение координаты Уmax мяча) и скорость мяча в момент его падения на землю. (рис 7)

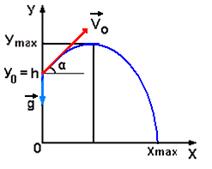
рис.7

Решение задачи начинается с выбора начала отсчёта, с которым совмещают начало системы координат ХОУ. Удобно начало отсчета и связанное с ним начало координат выбрать на поверхности земли под балконом, направив оси Х и У соответственно горизонтально и вертикально. Отмечаем на оси У начальную координату мяча У0 = h, направляем вектор начальной скорости V0 под углом α к горизонту и изображаем траекторию полёта мяча, которая, представляет собой параболу. Точка пересечения параболы с осью Х определит координату Xmax, значение которой даст дальность полёта мяча. Наибольшая высота полёта мяча определится значением координаты Уmax вершины параболы. Для составления уравнений движения Х=Х (t) и У=У (t) имеет смысл записать составляющие этих уравнений:

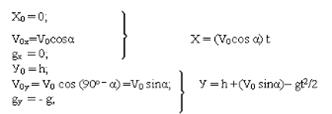
Через время tп (время полёта мяча) координаты мяча примут значения: Х =Хmax, у = 0. Тогда уравнения примут вид:

Хmax=V0 (cosα) tп; 0=h+ (V0sinα) tп-gtп2/2.

Решая последнее квадратное уравнение, находим время полёта мяча tп.

tп= [V0sinα+ (V02sin2α+ 2gh) 1/2] /g,

которое имеет только одно значение. Второе - отрицательное значение tп, которое следует из решения квадратного уравнения, не возможно. Здесь и далее корень квадратный из числа записывается как это число в степени ½.

Подставив значение tп в уравнение определим дальность полёта мяча Хmax.

Хmax=V0 (cosα) =V0 (cosα) [V0 sin α + (V02 sin2α + 2gh) 1/2] /g.

В верхней точке траектории мяча высота его полёта максимальна, а проекция скорости на ось ОУ равна нулю. Для продолжения решения необходимо перейти к уравнениям проекций скорости V на оси Х и У как функциям времени. Взяв производные по времени от уравнений движения, получаем:

Vx=V0cosα; Vy=V0sinα-gt.

Первое уравнение показывает, что вдоль оси ОХ мяч летит равномерно с постоянной скоростью, не зависящей от времени. Движение мяча вдоль оси ОУ является равнопеременным (при движении до верхней точки полёта - равнозамедленным, а затем становится равноускоренным). В момент времени tв (время полёта мяча до верхней точки) проекция скорости Vy становится равной нулю, а координата У принимает максимальное значение уmax.

Информация по теме:

Психолого-педагогическая характеристика детей старшего дошкольного возраста
В данном параграфе рассмотрим психолого-педагогическую особенность детей старшего дошкольного возраста. Как показал анализ литературы по данной проблеме (А. Валлон, А.Л. Венгер, Р.Я. Гузман, В.В. Давыдов, А.В. Запорожец, Я.Л. Коломинский, Г.Г. Кравцов, Е.Е. Кравцова, В.В. Рубцов, Л.М. Фридман, Г.А. ...

Реализация курса для пятого класса школы №320 г. Красноярска
Программа курса «Университетское образование» была реализована частично в школе №320 г. Красноярска. Первые три занятия были посвящены знакомству. На первом занятии курса «Университетское образование», которую вел Васильев Виктор Георгиевич, было зафиксировано нами, что дети в этом возрасте не могу ...

Психокоррекционные методы и группы ,возможности их использования педагогической практике
Психокоррекция возникла в рамках специализации психологии и дефектологии. Первый период - описательный, связан с описанием медицинских наук и педагогических вопросов коррекции аномального развития. Э. Сеген предложил комплексный подход к воспитанию умственно отсталых детей и описал оригинальные мет ...