Методы решения физических задач

Разделив обе части равенства на р2, получим искомое соотношение импульсов 1 - (р1/р2) = 1/3 + (р1/р2).

Откуда р1/р2 = 1/3.

Задача: Космический корабль обращается вокруг Луны по круговой орбите, радиус которой равен трём радиусам Луны (R = 3Rл). Какую минимальную скорость нужно сообщить спускаемому аппарату, чтобы он прилунился на противоположной стороне Луны? (рис.15)

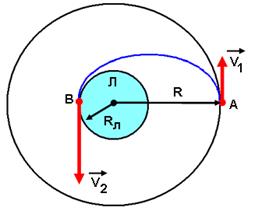
рис.15

Сначала определим скорость V0 космического корабля при его движении вокруг Луны по круговой орбите радиуса R, используя второй закон Ньютона: G Mm/R2 = mV02,где М - масса Луны, m - масса космического корабля, G - гравитационная постоянная.

Отсюда V0= (GM/R) 1/2= (GM/3Rл) 1/2.

Подставив в формулу значения гравитационной постоянной, массы и радиуса Луны, взятые из справочника (G = 6,672 10-11 Hм2/кг2, М = 7,35 1022кг, Rл = 1737 км) получаем значение этой скорости: V0 = 970 м/с.

Чтобы прилуниться в точке В, космический аппарат должен двигаться по эллиптической орбите (рис.15), а для этого его скорость должна измениться и стать равной V1. При движении по этой траектории выполняются законы сохранения момента импульса и энергии:

mV1R=mV2Rл;

mV12/2-GMm/R=mV22/2-GMm/Rл.

Спускаемый аппарат обладает как кинетической энергией, вследствие движения, так и потенциальной энергией, вследствие гравитационного взаимодействия с Луной.

Видоизменим полученную систему уравнений, учитывая, что R = 3Rл.

3V1 = V2;

V12-2GM/3Rл=V22-2GM/Rл.

Решая полученную систему уравнений относительно V1, получаем выражение для скорости, которая обеспечит начало движения спускаемого аппарата по эллиптической орбите V1= (GM/6Rл) 1/2.

Подставив в формулу значения гравитационной постоянной, массы и радиуса Луны получаем значение этой скорости: V1 = 686 м/с.

Сравнение скоростей V0 и V1 показывает, что V1 < V0, следовательно, чтобы изменить скорость спускаемого аппарата от V0 до V1, ему нужно сообщить скорость V в направлении, противоположном вектору скорости V0, равную

V = V0 - V1 = 970 - 686 = 284 м/с

Для сообщения этой скорости спускаемому аппарату, его нужно развернуть двигательной установкой по движению корабля и включить её.

Метод отрицательных масс

Этот метод используется при решении задач на определение положения центра масс фигуры, имеющей удалённые из неё участки. В этом случае массу удалённого участка считают отрицательной, а силу тяжести этого участка (-mg) направляют вверх. В дальнейшем используют условие равновесия тела, находящегося под действием системы параллельных сил. Здесь используется понятие момента силы.

Задача: Определить координату ХС центра масс однородного цилиндра радиуса R, в котором высверлено сквозное цилиндрическое отверстие радиуса r, ось которого параллельна оси цилиндра и находится от неё на расстоянии d.

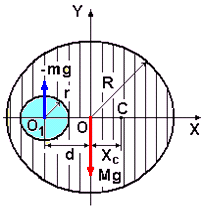
рис.16

Изобразим поперечное сечение цилиндра с высверленным в нём цилиндрическим отверстием. Сечение проводим через середину длины цилинра. Центр масс (точка С) (рис.16) находится на оси Х, проходящей через точки О и О1. После удаления цилиндрической части радиуса r он смещается вправо от оси основного цилиндра. На рисунке указываем силы тяжестей сплошного цилиндра Mg и удалённого цилиндра (-mg). Под действием этих сил цилиндр остаётся в равновесии, если ось вращения проходит через центр масс. Условие равновесия тела, имеющего ось вращения заключается в равенстве нулю суммы моментов сил, приложенных к телу, относительно этой оси.

Условие равновесия будет иметь вид: Mg XC - mg (d + XC) = 0.

Массы М и m определим по формулам:

М=ρV=ρπR2L; m=ρ π r2L,

где ρ - плотность материала цилиндра, L - длина цилиндра.

После подстановки масс в условие равновесия и преобразований получаем выражение: R2XC-r2 (d-XC) =0,Откуда получаем значение координаты центра масс ХС: ХС=d [r2/ (R2+r2)].

Задача: Определить координату центра масс алюминиевого цилиндра радиуса R, в котором сквозное высверленное цилиндрическое отверстие радиуса r залито свинцом.

Расстояние между осями алюминиевого цилиндра и заполненного отверстия d.

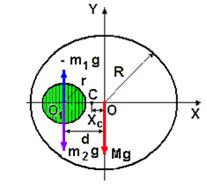
рис.17

Поскольку плотность свинца больше плотности алюминия, то центр масс (точка С) такого цилиндра сместится влево от оси основного цилиндра. Масса высверленного алюминиевого цилиндра m1 считается отрицательной, поэтому сила тяжести (-m1g) направлена вверх, а сила тяжести заполняющего это отверстие свинца m2g направлена, как обычно, вниз (рис.17).

Информация по теме:

Опыт реализации методики проведения деловой игры по дисциплине «Экономика» учащихся 11 класса
Опираясь на разработанную методику организации деловых игр в первой главе, перейдем к выполнению главной задачи – разработке комплекса деловых игр по экономике для учащихся 11 класса. В данной работе в качестве примера будут приведены игры на темы «Семейная экономика» и «Фирма». Деловая игра по тем ...

Основное содержание умений, интеллектуального компонента культуры умственного труда и способы их формирования
Уровень культуры умственного труда школьников определяет все стороны и результаты обучения: качество формируемых знаний и умений; познавательную активность учащихся и развитие их мышления, творческих сил; производительность учебного труда и зависящий от неё уровень учебной нагрузки; эффективность и ...

Проблемно-поисковые методы обучения
Отличительной чертой проблемно-поисковых методов является постановка перед обучающимися вопроса (проблемы), на который они самостоятельно ищут ответ, как бы сами создают новые знания, "делают открытия", формулируют теоретические выводы. Проблемно-поисковые методы требуют активной мыслител ...