Методы решения физических задач

Задача: Найти сопротивление цепи, изображённой на рис.26, а, если сопротивления всех резисторов одинаковы и равны R.

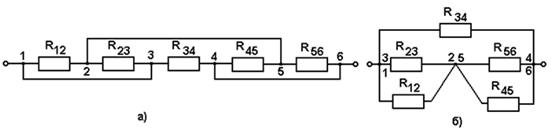
рис.26

Потенциалы точек 1 и 3 одинаковы, поэтому их можно объединить в одну, то же самое можно сделать с точками 2 и 5, 4 и 6. В результате получится видоизменённая упрощённая схема (рис.26, б).

Резисторы R12 и R23 соединены параллельно, следовательно, их общее сопротивление равно R/2. Точно также общее сопротивление резисторов R45 и R56 равно R/2. Общее сопротивление части цепи параллельной R34 равно R/2 + R/2 = R, поэтому сопротивление всей цепи будет равно R/2.

4.6.4 Метод разделения узлов.

Метод разделения узлов схемы основан на том, что, если возможно объединение двух узлов, имеющих равные потенциалы, то возможен и обратный переход: узел схемы можно разделить на две или несколько точек, если получившиеся при этом точки имеют прежние одинаковые потенциалы.

Задача: Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис.27) сопротивлением R каждый.

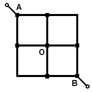
рис.27

Разделим узел О на две точки, получив два варианта электрической цепи (рис.28, а) и (рис.28, б). В первом случае потенциалы точек О’ и О’’ не равны., Если потенциал точки А больше потенциала точки В, то потенциал точки О’ больше потенциала точки О’’ и наоборот. Потенциалы же точек О1 и О2 равны, так как находятся в одинаковых условиях (полностью симметричны). Отсюда следует, что верным является разделение узла О, показанное на рис.28, б. Эквивалентная схема цепи, полученная после разделения узла О, изображена на рис.28, в. Отсюда общее сопротивление цепи между точками А и В равно 3R/2.

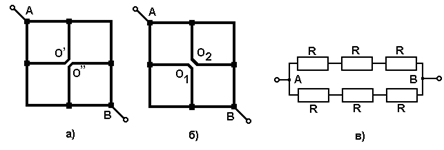
рис.28

Задача: Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис.29, а) сопротивлением R каждый.

Единственно верным способом разделения узла О на отдельные точки О1, О2 и О3 является способ, изображённый на рис.29, б. Эквивалентное сопротивление участков (cd) и (ef) будет равноRcd=Ref=2RR/ (2R+ R) =2R/3.

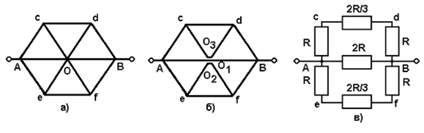
рис.29

Эквивалентное сопротивление участка АО1В равно 2R. Эквивалентная схема цепи, полученная после разделения узла О, изображена на рис.29, в. Общее сопротивление цепи определим по формуле:

1/Rобщ=3/8R+3/8R+1/2R=5/4R, откуда Rобщ = 4R/5.

Метод преобразования и расчёта цепей с помощью перехода "звезда" - "треугольник".

Этот метод основан на том, что схему, имеющую три узла, можно заменить другой, с тем же числом узлов. При этом сопротивление участка между двумя любыми узлами новой схемы должно быть равно сопротивлению заменяемого участка. В результате получается схема, сопротивление которой эквивалентно сопротивлению данной по условию. Поскольку в результате такого преобразования изменяются токи внутри цепи, то такую замену проводят в тех случаях, когда не нужно находить распределение токов.

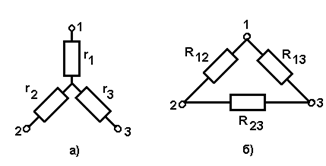
рис.30

Рассмотрим преобразование схем, имеющих три вывода (трёхполюсников).

Это преобразование называется преобразованием "звезды" (рис.30, а) в "треугольник" (рис.30, б), и наоборот.

В "звезде" сопротивление между точками 1 и 2 равно r1 + r2, в "треугольнике" R12 (R13 + R23) / (R12 + R13 + R23). Следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо выполнение равенства:

r1+r2=R12 (R13+R23) / (R12+ R13 + R23).

Аналогично для точек 1 и 3 и для точек 2 и 3:

r1+r3=R13 (R12+R23) / (R12+ R13 + R23).

r2+r3=R23 (R12+R13) / (R12+ R13 + R23).

Сложив левые и правые части этих уравнений и разделив полученные суммы на 2, получим:

r1+r2+r3= (R12R13 +R12 R23 + R13 R23) /) / (R12 + R13 + R23).

После преобразований получим:

r1=R12R13/ (R12+R13+R23);

r2=R12R23/ (R12+R13+R23);

r3=R13R23/ (R12+R13+R23).

Аналогично получаются формулы для обратного преобразования:

R12= (r1r2+r1r3+r2r3) / r3;

R13= (r1r2+r1r3+r2r3) / r2;

R23= (r1r2+r1r3+r2r3) / r1.

Задача: Определите сопротивление цепи АВ (рис.31. а), если R1=R5= 1 Oм; R2=R6=2Oм; R3=R7=3 Oм; R4=R8 =4 Oм.

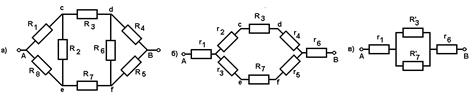
рис.31

Преобразуем "треугольники" R1 R2 R8 R4 R5 R6 в эквивалентные "звёзды", тогда схема примет вид, изображённый на рис.35, б. Сопротивления r1, r2, r3, … r6 рассчитаем по формулам: r1 = R1 R8/ (R1 + R2 + R8) = 4/7 Ом;

Информация по теме:

Репродуктивные методы обучения
Как и всякая система обучения, сообщающее обучение имеет специфические цели, содержание и методы. Ряд общих задач обучения весьма успешно решается именно с его помощью. Но некоторые другие задачи, и притом важные, эта система решает неполно или вовсе не решает. Цели сообщающего обучения – обогащени ...

Роль семьи в экологическом воспитании детей старшего дошкольного возраста
Практическая работа проведена на базе ДОУ ЦЦР № 138 Краснодарского края, при участии родителей детей подготовительной группы № 3 в количестве 13 человек. Практическая работа направлена на определение того, как семья влияет на воспитание в своих детях экологической культуры и в чем проявляется их ра ...

Особенности овладения словообразованием детьми дошкольного возраста в онтогенезе
Основополагающее значение для понимания грамматического строя и словообразования в частности имеют работы А.Н. Гвоздева, С.А. Рубинштейна, Д.Б. Эльконина. В исследованиях известного лингвиста А.Н. Гвоздева собран уникальный фактический материал. Формирование лексики у ребенка тесно связано с процес ...