Методы решения физических задач

r2 = R1 R2/ (R1 + R2 + R8) = 2/7 Ом; r3 = R2 R8/ (R1 + R2 + R8) = 8/7 Ом;

r4=R4R6/ (R4+R5+R6) =8/7Ом; r5 = R5 R6/ (R4 + R5 + R6) = 2/7 Ом;

r6 = R4 R5/ (R4 + R5 + R6) = 4/7 Ом;

Схема, изображённая на рис.31, в является эквивалентной схеме на рис.31, б. Здесь R’3 = r2 + R3 + r4 = 31/7 Ом; R’7 = r3 + R7 + r5 = 31/7 Ом, R’3 = R’7. Общее сопротивление цепи

Rобщ = r1 + R’3/2 + r6 = 47/14 Ом.

Задача: Определить общее сопротивление неуравновешенного моста (рис.32, а), если R1 = 1,0 Oм; R2 = 1,6 Oм; R3 = 2,0 Oм; R4 = 1,2 Oм; R5 = 2,0 Oм.

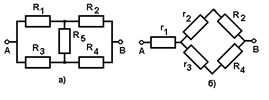
рис.32

Если преобразовать "треугольник" из резисторов R1, R3, R5 в эквивалентную "звезду", то получится простая схема (рис.32, б). Рассчитаем сопротивления r1, r2 и r3 по формулам:

r1 = R1R3/ (R1 + R3 + R5) = 0,4 Ом; r2 = R1R5/ (R1 + R3 + R5) = 0,4 Ом; r3 = R3R5/ (R1 + R3 + R5) = 0,8 Ом;

Общее сопротивление цепи

Rобщ = r1 + (r2 + R2) (r3 +R4) / (r2 + R2 + r3 + R4) = 1,4 Ом.

Векторный метод решения задач

Этот метод используется в случае, если при сложении векторов получается замкнутый треугольник. Это может быть треугольник скоростей, сил, импульсов, напряжённостей электрических и индукций магнитных полей.

Задача: Мальчик и девочка решили попасть из пункта А в пункт В, расположенные на противоположных берегах реки, скорость течения которой u. Мальчик плывёт так, чтобы сразу оказаться в пункте В. Девочка направляет скорость своего плавания поперёк скорости течения реки и, чтобы попасть в пункт В, должна пройти по противоположному берегу то расстояние, на которое её снесёт течением. С какой скоростью должна перемещаться девочка по берегу, чтобы оказаться в пункте В одновременно с мальчиком? Скорости и мальчика, и девочки относительно воды одинаковы и равны V.

При решении используем закон сложения скоростей, согласно которому скорость тела относительно неподвижной системы отсчёта равна сумме скорости относительно подвижной системы и скорости самой подвижной системы. На рис.33, а показана скорость мальчика V1 относительно берегов, которая получается путём сложения скорости мальчика относительно воды V и скорости течения реки u. Модуль скорости V1 определим по теореме Пифагора: V1= (V2 - u2) 1/2.

Время, за которое мальчик сумеет переплыть реку по прямой АВ, определим по формуле: t1 = L/V1, L - ширина реки.

На рис.33, б показана скорость девочки V2 относительно берегов реки, которая также равна сумме векторов скоростей девочки относительно воды V и течения реки u. Однако по модулю она равна V2= (V2+u2) 1/2.

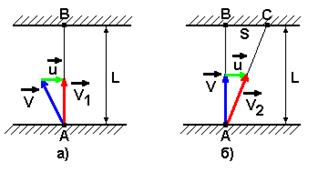
рис.33

Время, которое потребуется девочке, чтобы переплыть реку по прямой АС равно:

t2=L/V,

т.к. вдоль прямой АВ она плывёт со скоростью V. Поскольку V > V1, то t2 < t1 на величину

Δt = t1 - t2 = L (1/V1 - 1/V).

Девочка приплывает в пункт С и, чтобы попасть в пункт В вместе с мальчиком ей требуется перемещаться по прямой ВС со скоростью V ‘ = S/ Δt, где S - длина прямой ВС, представляющая собой расстояние, на которое сносит девочку течение реки. Из подобия векторного треугольника и треугольника АВС (рис.33, б) составим пропорцию S/L = u/V, откуда найдём S:

S = Lu/V.

Скорость перемещения девочки по прямой ВС будет равна: V ‘= S/Δt= Lu/VΔt или после подстановки значения Δt и V1:

V ‘=u/V (1/V1-1/V) =u/V [1/ (V2 - u2) 1/2 - 1/V].

Задача: (стр.17) можно решить не только координатным методом, но и векторным.

На шарик действуют силы: mg - сила тяжести, FA - архимедова сила, T - сила натяжения нити и FE - сила, действующая на заряд шарика со стороны электрического поля (рис.9).

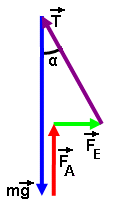
рис.34

Произведя сложение векторов этих сил, получим векторный треугольник со сторонами (mg - FA), FE и Т.

По условию равновесия сумма векторов сил должна быть равна нулю, поэтому конец вектора Т должен совпасть с началом вектора mg (рис.34). Так как сила натяжения направлена вдоль нити, а сила тяжести вертикально вниз, то между ними будет угол α. Угол между векторами mg и FE прямой. Отношение противолежащего катета к прилежащему для угла α равно тангенсу этого угла: tgα=FE/ (mg-FA).

Метод решения обратной задачи

Многие физические явления, изучаемые в школьном курсе физики, рассматриваются в идеальных условиях.

При рассмотрении механических явлений часто пренебрегают сопротивлением среды, трением, рассеянием энергии, поэтому такие явления носят обратимый характер. Для таких случаев направление прямого процесса можно заменить обратным процессом.

Информация по теме:

Рекомендации по использованию компьютерных программ и техника безопасности при работе с ними
Занятия на компьютере должны быть комплексными. Они включают в себя 3 этапа. I этап - подготовительный. Идет погружение ребенка в сюжет занятия, период подготовки к компьютерной игре через развивающие игры, беседы, конкурсы, соревнования, которые помогут ему справиться с поставленной задачей. Включ ...

Изучение жизни и творчества С. Есенина на завершающем этапе литературного образования
Эпиграфом к общей теме "Сергей Есенин. Жизнь и творчество" могут стать слова А. Серафимовича "Это был великий художник. С огромной интуицией, с огромным творчеством, единственный в наше время поэт. Такой чудовищной способности изображения тончайших переживаний, самых нежнейших, самых ...

Использование традиций костюма русских крестьян Южного Алтая на уроках технологии
В качестве базисной основы содержания трудового обучения в начальных классах средних школ взято ознакомление с декоративно-прикладным творчеством своего народа. Народное искусство открывает человеку его прошлое, знакомит с представлениями о прекрасном, эстетическим опытом предшествующих поколений, ...