Методы решения физических задач
Метод составления системы уравнений
Система идентичных уравнений.
Метод используется при решении тех задач, в которых рассматривается одно и то же физическое явление, происходящее при разных условиях, отражённых в данных задачи. При составлении уравнений необходимо проанализировать, какие физические величины, описывающие это явление, остаются одинаковыми.
Задача: Эскалатор (движущаяся лестница) спускает идущего по нему пассажира за время t1, а движущегося по нему в два раза быстрее за время t2. За какое время эскалатор спускает стоящего на нём пассажира?
В этой задаче одинаковыми являются длина эскалатора S и скорость его движения u. Скорость первого пассажира в неподвижной системе отсчёта по закону сложения скоростей складывается из скорости пассажира относительно эскалатора v и скорости самого эскалатора u: v1=v+u, её также можно определить по определению скорости v1=S/t1. Тогда для скорости движения первого пассажира получим соотношение: S/t1=v+u.
Аналогично для скорости движения второго пассажира, который движется относительно эскалатора со скоростью 2v: S/t2=2v+u.
Для третьего пассажира уравнение скорости движения будет иметь вид: S/t3=u.
В системе трёх уравнений четыре неизвестных: S, v, u и искомое t3, поэтому необходимо понизить число неизвестных. Для исключения неизвестной скорости v, вычтем второе уравнение из первого уравнения, умноженного на 2. В результате чего получим уравнение: S (2/t1-1/t2) =u.
Далее решаем систему из третьего и последнего уравнений. Приравняв левые части этих равенств, и сократив на S, получим выражение: 2/t1-1/t2=1/ t3.
Откуда t3= t1t2/ (2t2-t1).
Задача: Посередине откачанной и запаянной с обоих концов трубки длиной L, расположенной горизонтально, находится столбик ртути длиной h. Если трубку поставить вертикально, то столбик ртути сместится на расстояние равное d. До какого давления была откачана трубка? Плотность ртути ρ.
Процесс перевода трубки из горизонтального положения в вертикальное (рис.13) можно считать изотермическим, и, следовательно, к состояниям газа в обеих частях трубки применить закон Бойля-Мариотта.
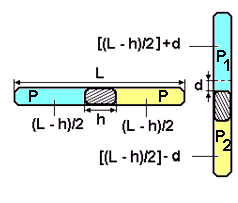
рис.13
Поскольку площадь поперечного сечения трубки остаётся постоянной, то объёмы частей трубки, занятые газом, пропорциональны их длинам. Тогда для газа в верхней части трубки закон Бойля-Мариотта запишется так:
Р (L - h) /2 = P1 [ (L - h) /2 + d];
а для газа в нижней части трубки - Р (L - h) /2 = P2 [ (L - h) /2 - d]. Здесь Р1 и Р2 - давления газа в верхней и нижней частях трубки соответственно, которые связаны между собой соотношением: Р2-Р1=ρgh.
Решая полученную систему из трех уравнений относительно давления газа Р в обеих частях трубки при её горизонтальном положении, получаем
Р = ρgh [ (L - h) 2 - 4d2] (L - h) d.
Система уравнений законов сохранения.
При столкновении тел (ударе) всегда выполняется закон сохранения импульса, вне зависимости от вида удара упругого или неупругого. Закон сохранения механической энергии выполняется при абсолютно упругом ударе, при неупругом - часть механической энергии переходит во внутреннюю энергию.
При движении тел по замкнутым криволинейным траекториям (окружность, эллипс) в отсутствии силы сопротивления выполняются законы сохранения момента импульса и энергии.
Задача: Два шарика массами m и 3m висят, соприкасаясь, на длинных нерастяжимых нитях. Шарик меньшей массы вместе с нитью, на которой он подвешен, отклоняют на угол 90о и шарик отпускают. Определить отношение импульсов (р1/р2) шариков после столкновения. Удар считать абсолютно упругим.
Пусть первый шарик массой m в самый последний момент до удара со вторым шариком массой 3m имеет импульс р. После удара импульс первого шарика р1 направлен противоположно, потому что его масса меньше массы второго. Второй шарик имеет импульс р2 (рис.14).
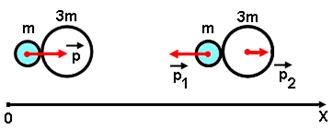
рис.14
Запишем выражение закона сохранения импульсов шариков в проекциях импульсов на координатную ось 0Х: р=р2-р1.
Это уравнение содержит два неизвестных р1 и р2. Запишем второе уравнение, в которое входили бы эти же неизвестные. Это уравнение закона сохранения энергии (в данном случае кинетической энергии), которая сохраняется, вследствие абсолютно упругого удара: р2/2mр12/ 2m+ р22/ 6m.
Здесь используется формула, связывающая кинетическую энергию с импульсом. Приведём систему из двух уравнений к следующему виду:
р + р1 =р2
р2-р12=р22/ 3.
После деления второго уравнения системы на первое получим выражение: р - р1 = р2/3, которое решаем совместно с уравнением р=р2-р1. Получаем соотношение: р2-р1=р2/3+р1.
Информация по теме:
Методические разработки по изучению "Web
конструирования" в школьном курсе информатики и ИКТ
Одна из задач школы - содействовать воспитанию нового поколения, отвечающего по своему уровню развития и образу жизни условиям информационного общества. Для этого учащимся предлагается осваивать способы работы с информационными потоками - искать необходимую информацию в доступных источниках, анализ ...
Программа элективного курса по математике
«Основы теории вероятностей и математической статистики» Элективный курс «Основы теории вероятностей и математической статистики» разработан для обеспечения старшеклассников занятиями по выбору из вариативного компонента базисного учебного плана в старшей профильной школе. Предлагаемый элективный к ...
Особенности психического и физического развития детей с нарушениями
интеллектуального развития
Дети с нарушениями интеллектуального развития характеризуются стойкими нарушениями всей психической деятельности, особенно отчетливо обнаруживающимися в сфере познавательных процессов. Причем имеет место не только отставание от нормы, но и глубокое своеобразие личностных проявлений, и познания. Так ...
Навигация
- Главная
- Методы обучения
- Семейное воспитание
- Роль игры в воспитании
- Знания, навыки и умения в процессе обучения
- Влияние среды на развитие личности ребёнка
- Нравственное воспитание в современном мире
- Педагогика
