Методы решения физических задач

Массы М, m1 и m2 определим по формулам:

М = ρAlπR2L; m1 = ρAlπr2L; m2=ρPbπr2L.

Уравнение равновесия цилиндра относительно оси, проходящей через центр масс, будет иметь вид:

m2g (d-XC) - m1g (d-XC) - MgXC =0.

После подстановки значений М, m1 и m2 в уравнение равновесия и преобразований получим выражение, определяющее координату центра масс данного цилиндра:

XC=dr2 (ρPb-ρAl) / [ρAl (R2-r2) + ρPbr 2].

Метод индукции

Этот метод подобен методу математической индукции, с помощью которого устанавливается общая зависимость некоторых величин по их частным зависимостям.

Задача: Гоночный автомобиль ("болид") движется равноускоренно из состояния покоя. На первых десяти метрах его скорость возрастает на 10 м/с. Определить возрастание его скорости на тех же десяти метрах при прохождении от 990-го метра до 1000-го метра пути и сравнить с возрастанием на первых десяти метрах. Дать объяснение их значительному расхождению.

При решении задачи используем соотношение между изменением скорости и пройденным путём: V2-V02=2aS.

Скорость автомобиля после прохождения первого десятиметрового отрезка (S = 10 м) определится соотношением: V12=V02 + 2aS =0 +2aS =2aS;

после прохождения второго: V22= V12 + 2aS=2aS+2aS=4aS=2V12;

после прохождения третьего: V32=V22 +2aS=4aS+2aS = 6aS = 3V12;

Следовательно, между обеими частями трех последних равенств просматривается зависимость вида: Vn2= nV12,откуда связь между скоростью при прохождении n-го десятиметрового отрезка и первого выразится соотношением: Vn= (n) 1/2V1. Используя это соотношение определим скорость после прохождения 99 - го и 100 - го десятиметровых отрезков, соответственно, V99= (99) 1/2V1, V100= (100) 1/2V1; тогда возрастание скорости на десятиметровом отрезке между 990 м и 1000 м пути составит: Δ V (99 - 100) = [ (100) 1/2- (99) 1/2] V1≈0,5 (м/с).

На первых десяти метрах скорость возросла на 10 м/с, а на сотом таком отрезке пути всего на 0,5 м/с. Это потому, что при прохождении сотого отрезка длиной в 10 м скорость автомобиля составляет около 100 м/с (360 км/ч), и "болид" проскакивает эти десять метров за очень малый промежуток времени, в течение которого и скорость увеличивается незначительно. Так как при равноускоренном движении ΔV = a Δt, то время проскакивания "болидом" этих десяти метров составит Δt = ΔV (99 - 100) /a. Ускорение можно определить как: а = V12/ 2S = 102/ (2.10) = 5 м/с2,тогда Δt = 0,5 м/с / 5 м/с2 = 0,1 с.

Задача: Поршневым вакуумным насосом (рис.22) с рабочей камерой объёмом ΔV откачивают воздух из сосуда объёмом V от давления P0 до давления Рn (Pn< P0). Определить число n ходов поршня, которое должно быть совершено при этом. Процесс откачки считать изотермическим.

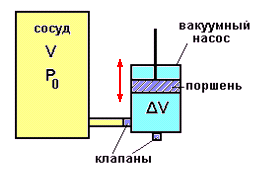
рис.18

Вакуумный насос - это устройство, которое при работе создаёт в объёме своей рабочей камеры ΔV пониженное давление (порядка 10 - 3 - 10-4 мм рт. ст.)

Поэтому при подключении насоса к откачиваемому объёму общий объём становится равным V + ΔV, газ расширяется, заполняя оба объёма, и понижает своё давление.

Тот газ, который заполняет рабочую камеру насоса, отсекается насосом и выталкивается в атмосферу. "Пустой" объём рабочей камеры вновь подключается к откачиваемому объёму.

Происходит очередное расширение газа, приводящее к очередному понижению давления, и т.д.

Так как процесс считается изотермическим, то, используя закон Бойля - Мариотта, можно для начального состояния газа в откачиваемом объёме и состояния газа после первого подключения рабочей камеры насоса записать уравнение:

Р0V=P1 (V+ΔV),

из которого определим давление в сосуде после первого хода поршня насоса

Р1=Р0V/ (V+ΔV).

Тогда после второго подключения можно записать уравнение: Р1V=P2 (V+ΔV), откуда определим давление в сосуде после второго хода поршня насоса:

Р2 = Р1V / (V+ΔV) =Р0 [V/ (V+ΔV)] 2.

Аналогично для третьего хода поршня вакуумного насоса: Р2 V = P3 (V + ΔV),

P3 = Р2 V / (V+ΔV) =Р0 [V/ (V+ΔV)] 3.

Из анализа уравнений просматривается зависимость, связывающая давление в сосуде после n-го хода поршня Pn c первоначальным давлением Р0:

Pn=Р0 [V/ (V+ΔV)] n.

Для нахождения числа ходов поршня n логарифмируем уравнение:

lg Pn = lg P0+nlg [V/ (V+ΔV)], откуда n = lg (Pn/P0) /lg [V/ (V+ΔV)].

При достижении в откачиваемом объёме давления равного давлению в рабочей камере насоса (10 - 3 - 10 - 4 мм рт. ст.) процесс откачки прекращается и насос лишь поддерживает достигнутый вакуум.

Информация по теме:

Роль педагога в развитии креативности старших дошкольников в игре
В данном параграфе мы попытаемся выяснить роль педагога в развитии творческих способностей у дошкольников в игре. Нам необходимо остановиться на традиционных подходах к рассмотрению данной проблемы. При этом особое внимание уделить тем педагогическим условиям, которые специфически влияют на развити ...

Организация самостоятельной работы в процессе обучения информатике
В психолого-педагогической литературе самостоятельность обычно понимается как способность личности к деятельности, совершаемой без вмешательства со стороны. Самостоятельная познавательная деятельность учеников может носить как характер простого воспроизведения, так и преобразовательный, творческий. ...

Задача учителя – донести до сознания ребенка народную мудрость
1. Сказка для ребенка имеет большое воспитательное и познавательное значение. Это любимый жанр многих детей. И не случайно в программу начальной школы включены различные сказки. Так в первом классе учащиеся знакомятся со сказками о животных, читают бытовые и волшебные сказки («Лиса и тетерев»; «Два ...