Методы решения физических задач

Результат получен после поворота и второго конца на угол . Искомая работа равна половине работы по перемещению доски на L.

Задача: В полусферический колокол, плотно лежащий на столе, наливает через отверстие вверху воду. Когда вода доходит до отверстия, она приподнимает колокол и начинает вытекать снизу. Радиус колокола R, плотность воды . Найти массу колокола М. (рис.37)

1-й способ. Прямое динамическое решение задачи (рис.41, а) F=Mg+. F=, M= 2-й способ. Поместим систему в цилиндрический сосуд высотой и радиусом R. (рис.37, б)

Пусть колокол тонок и его масса мала. Давление на колокол снаружи и изнутри равно во всех точках. Если колокол убрать, то

M= () , M= () =

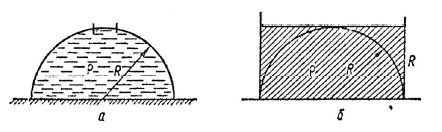
рис.37

Задача: Найти кинетическую энергию стержня, вращающегося в горизонтальной плоскости вокруг вертикальной оси, проходящей через его середину. Известны: (рис.38, а)

Для половины стержня (рис.38, б) . Но К=2, следовательно К=.

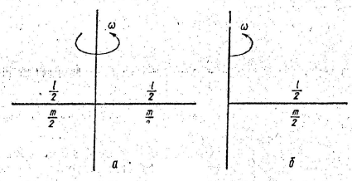
рис.38

Для того чтобы в полной мере овладеть использованием вышеизложенного метода необходимо решить не одну задачу с применением данного метода.

Метод дифференцирования и интегрирования

В основе метода лежат два принципа:

1) принцип возможности представления закона в дифференциальной форме;

2) принцип суперпозиции.

При использовании метода дифференцирования и интегрирования, разделяют тело на материальные точки или траекторию и время на такие промежутки, на которых процесс можно считать равномерным. Далее по принципу суперпозиций производят суммирование (интегрирование).

Задача: Найти силу гравитационного взаимодействия между расположенными на одной прямой материальной точкой массой m и однородным стержнем длиной L и массой M. Расстояние от точки до ближайшего конца стержня равно С. (рис.39)

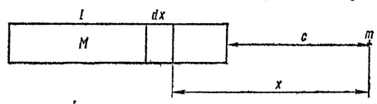
рис.39

Выделяем на расстоянии х от точки элемент стержня длиной dx и массой dx. Сила его взаимодействия с точкой dF=.

Поэтому F=.

Задача:

Найти кинетическую энергию однородного диска радиусом R и массы M, вращающегося с постоянной угловой скоростью вокруг оси, проходящей через центр диска перпендикулярно его плоскости.

Разобьем диск на кольца шириной dx, каждое из которых отстоит от оси вращения на x [0: R]. Масса каждого кольца, вращающегося с линейной скоростью

: dm=

Величиной (dx) 2 в сравнении с 2xdx можно пренебречь.

dk=

Откуда К=

Метод дифференцирования и интегрирования применяется также для вывода формул.

Вариационные принципы механики, метод виртуальных перемещений

Невариационные принципы устанавливают закономерности движения, совершаемого системой под действием приложенных сил.

Вариационные принципы разделяются на дифференциальные и интегральные. Дифференциальный - это метод виртуальных перемещений, интегральный - следствие из принципа наименьшего действия.

Принцип: Для равновесия любой механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ, действующих на систему сил при любом виртуальном перемещении, равнялась нулю.

Информация по теме:

Изучение уровня духовно-нравственного развития у младших подростков в современной общеобразовательной школе
Анализ возможностей русского православного искусства в духовно-нравственном развитии младших подростков предполагал определение состояния этой проблемы в школьной практике. Нами изучен и обобщен опыт работы многих учителей, педагогов дополнительного образования общеобразовательных школ г. Улан-Удэ, ...

Технология анализа произведений в их родовой специфике
Теперь, после того как сложилось представление об основных родах литературы, их задачах и особенностях, можно говорить более детально о технологии анализа художественных произведений разных литературных родов. Анализ эпического текста Сюжет является основой эпического текста, он его цементирует. Ра ...

Программа воспитания и обучения в детском саду
Дошкольное детство - это важнейший период в жизни человека, вся дальнейшая жизнь ребёнка будет определяться опытом, полученным в детстве. Сейчас все озабочены тем, чему научат ребёнка до школы. Конечно, это важно. Но гораздо важнее – как ребёнок проживёт эти годы, в какие игры будет играть, получит ...