Творческая тетрадь для шестого класса по теме “Признак делимости на 11 натуральных чисел”

Доказательство теоремы 2. По условию делится на при . Докажем, что число делится на .

Рассмотрим позиционную запись числа:

.

Из условия известно, что делится на . Выделим в позиционной записи числа слагаемое . Имеем:

. Полученное выражение делится на . Действительно, делится на по условию. Оставшиеся слагаемы, также делятся на .

Действительно, распишем при помощи формулы разности квадратов, 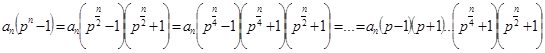. Видим, что один из множителей делится на значит, произведение делится на . Разложим в произведение двух множителей при помощи формулы суммы нечетных степеней формула заимствована из [5], получим . Видим, что один из множителей произведения делится на значит, произведение делится на , значит и делится на . Проведя аналогичные рассуждения для остальных слагаемых , , …, , получим, что они делятся на .

Итак, делится на , а значит, делится на .

Доказательство теоремы 2 для в точности повторяет доказательство теоремы 2 для .

Информация по теме:

Описание предметной области и ситуации
Моей системой, в которой возникла проблемная ситуация, является план создания студенческого портфолио. Обсуждение тематики создания и использования портфолио в вузе опирается на такие взаимоопределяющие тенденции в развитии российского образования, как: - Оформление постиндустриального общества рын ...

Возможности урока английского языка в развитии памяти младших школьников
В обширной литературе по дидактике, методике, педагогическим технологиям определение понятия «Урок», как правило, сводят к целостному, логически завершенному, ограниченному рамками примени отрезку образовательного процесса, в котором учебная работа проводится с постоянным составом учащихся примерно ...

Волевые качества личности младшего школьного возраста
Каждый период в жизни и развитии ребенка характеризуется определенным ведущим видом деятельности. В отечественной психологии под ведущей деятельностью понимается та, в процессе которой происходят качественные изменения в психике детей, происходит формирование основных психических процессов и свойст ...