Описание организационной формы передачи учителям методики работы с творческими работами

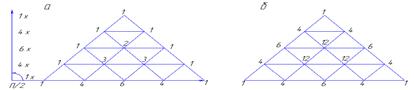
рис. 2.7

Получим разложение тринома . Для этого воспользуемся полученными формулами: формулой бинома Ньютона и формулой биномиальных коэффициентов.

В полученной формуле часть:

выражает основание треугольника Паскаля, т.е. триномиальные коэффициенты, которые лежат на внешней стороне -го сечения пирамиды. А часть полученной формулы: выражает триномиальные коэффициенты, лежащие внутри -го сечения пирамиды.

В литературе разложение тринома представляют в виде:

,

где - триномиальные коэффициенты, , , – неотрицательные целые числа, которые выражаются формулой:

Для триномиальных коэффициентов справедлива рекуррентная формула:

с начальными условиями ; .

Триномиальные коэффициенты удовлетворяют условиям:

и равенствам

,

указывающих на наличие трех осей симметрии.

Итак, наше исследование показало, что можно обобщить формулы квадрата суммы и куба суммы по степени, получив разложение формулы бинома Ньютона. Биномиальные коэффициенты можно найти либо при помощи треугольника Паскаля, записав коэффициенты разложения в виде треугольной таблицы и выведя очевидное правило, либо посредством формул числа сочетаний , которые возможно вывести. Также оказался возможным построение пирамиды Паскаля и вывод разложения для тринома. При этом нужно отметить, что если для вывода разложения бинома литература является средством подтверждения полученных результатов, то для разложения тринома литература является дополняющим средством к полученным результатам. Полученные результаты исследования были сопоставлены и дополнены материалом книг по этим вопросам.

Моя работа была направлена на разрешение проблем, возникающих у учителей, которые не имеют опыта работы с детскими творческими работами, но хотели бы заниматься ими со своими учениками. Для этого было разработано учебно-методическое средство, которое мы назвали творческой тетрадью – особым образом оформленная тетрадь, содержащая логику предъявления исследовательской задачи и специальным образом представленные задания. Используя эту тетрадь, учитель может освоить идею руководства детским исследованием в математике. Кроме этого, тетрадь также должна обеспечивать эмоциональную включенность и сохранение устойчивого интереса к теме у шестиклассника, инициировать возникновение у него своих вопросов, творческое отношение к предложенным задачам.

Информация по теме:

Организация самостоятельной работы учащихся в процессе обучения как педагогическая проблема
Существует множество различных направлений в исследовании природы активности и самостоятельности учащихся в обучении. Первое направление берет начало еще в древности. Его представителями можно считать еще древнегреческих ученых (Аристосен, Сократ, Платон, Аристотель), которые глубоко и всесторонне ...

Научно-теоретические основы констатирующего и формирующего экспериментов
Эксперимент означает пробу, опыт. Это один из основных методов научного познания вообще, психологического исследования в частности. Например, от наблюдения эксперимент отличается активным вмешательством в ситуацию со стороны исследователя, осуществляющего планомерное манипулирование одной или неско ...

Теоретическая интерпретация педагогического опыта
Ведущая идея опыта: Формирование правовой культуры учащихся на основе создания условий для творческого развития личности, формирование и становление ее гражданственности, раскрытие личности и ее интеграция в общество являются важными предпосылками для того, чтобы молодые люди стали самостоятельными ...