Описание организационной формы передачи учителям методики работы с творческими работами

Бином Ньютона можно обобщить по количеству слагаемых, т.е. найти разложение для , однако вывод данной формул является довольно сложным для школьника. Поэтому рассмотрим частный случай формулы, формулу для суммы трех переменных, т.е. для тринома. Выведем разложение для тринома , а также арифметическую таблицу триномиальных коэффициентов.

Рассмотрим ряд формул, являющихся частными случаями для , которые можно получить раскрыв скобки и приведя подобные слагаемые:

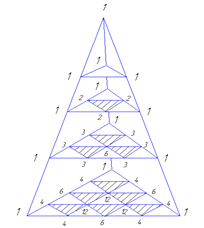
рис. 2.5

Построим арифметическую таблицу из триномиальных коэффициентов, данная таблица будет представлять собой пирамиду, которую называют пирамидой Паскаля (рис. 2.5). Видим, что по трем внешним ребрам пирамиды стоят единицы. Каждая из трех боковых граней представляет собой треугольник Паскаля. В n-ом сечении (треугольнике) пирамиды (n ≥ 0), параллельном основанию, располагаются триномиальные коэффициенты (которые обозначаются ) подобно биномиальным коэффициентам в треугольнике Паскаля.

Рассмотрим сечения пирамиды для , и (рис. 2.6):

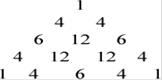
рис. 2.6

Видим, что коэффициенты, лежащие внутри сечения пирамиды в углу, равны сумме двух коэффициентов располагающихся на внешней стороне сечения, которые лежат на одной прямой с этим коэффициентом. Правило для нахождения триномиальных коэффициентов, стоящих внутри сечения пирамиды, вызвало большие трудности, поэтому правило вывода триномиальных коэффициентов было взято из литературы.

Известно, что любой внутренний элемент пирамиды Паскаля, стоящий в n -ом сечении, равен сумме трех элементов, расположенных в углах элементарного треугольника - го сечения пирамиды. Построение n-го сечения связывают с равенством :

;

Сечение получается из треугольника Паскаля, основанием которого служит -я строка треугольника, умножением элементов его строк почленно на элементы основания, повернутого против часовой стрелки на угол . Рис. 2.7, а иллюстрирует построение сечения при n=4. Расположение элементов сечения показано на рис. 2.7, .

Информация по теме:

Развитие речи дошкольников посредством сюжетно-ролевой игры
С целью повышения уровня развития речи, нами был разработан сборник сюжетно-ролевых игр, которые были направлены на обогащение активного словаря детей и развитие связной речи. Игры были отобраны с учетом возрастных возможностей и интересов детей. Данные игры проводились с детьми в течение 3 месяцев ...

Реализация курса для пятого класса школы №320 г. Красноярска
Программа курса «Университетское образование» была реализована частично в школе №320 г. Красноярска. Первые три занятия были посвящены знакомству. На первом занятии курса «Университетское образование», которую вел Васильев Виктор Георгиевич, было зафиксировано нами, что дети в этом возрасте не могу ...

Сущность механизма вероятностного прогнозирования
В предыдущем разделе были рассмотрены основные механизмы аудирования. Рассмотрим сущность механизма прогнозирования и его роль в процессе аудирования и понимания смысловой структуры текста. Механизм вероятностного прогнозирования подробно изучался в психологии и рассматривался в качестве одного из ...