Описание организационной формы передачи учителям методики работы с творческими работами

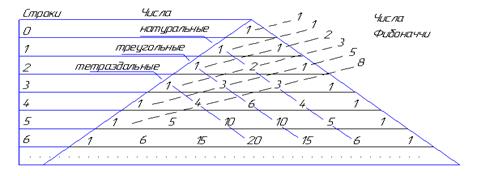
рис. 2.2

Таким образом, биномиальные коэффициенты можно найти при помощи треугольника Паскаля и выведенного правила. Однако этот способ не всегда удобен для получения биномиальных коэффициентов.

Разберем второй способ нахождения биномиальных коэффициентов, связанный с поиском числа сочетаний, которые принято обозначать или - число сочетаний из n по k элементов.

Рассмотрим известные формулы:

и

Раскроем скобки в правой части этих равенств, причем будем записывать все множители в том порядке, в котором они нам встретятся:

Видно, что в формулу квадрата суммы входят все сочетания, составленные из букв a и b по две буквы, а в формулу куба суммы – сочетания из тех же букв, но состоящие из трех букв каждое. То же самое будет и в общем случае:

мы получим всевозможные сочетания с повторениями букв x и y, состоящие из n элементов.

Теперь найдем формулу для получения числа сочетаний, т.е. биномиальных коэффициентов. Для этого рассмотрим уже известные формулы. Однако так как сочетания для x и y повторяются, то будем рассматривать сочетания по числу вхождений в них х.

Итак, для получаем, что в рассматриваемом множестве два элемента , тогда получаем число сочетаний из двух элементов по два равно единице (два элемента из двух мы можем выбрать только единственным образом); число сочетаний из двух элементов по одному равно двум, число сочетаний из двух элементов по нулю элементов равно единице: , , - биномиальные коэффициенты. Получили формулу:

Для получаем множество из трех элементов , тогда получаем, что число сочетаний из трех элементов по три равно единице ; число сочетаний из трех элементов по два равно трем , число сочетаний из трех элементов по одному равно трем , число сочетаний из трех элементов по нулю элементов равно . Получили формулу:

.

Информация по теме:

Применение моделирования для развития математических представлений старших дошкольников
Моделирование – наглядно-практический метод обучения. Модель представляет собой обобщенный образ существенных свойств моделируемого объекта (план комнаты, географическая карта, глобус и т.д.) Метод моделирования, разработанный Д.Б.Элькониным, Л.А.Венгером, Н.А.Ветлугиной, Н.Н.Поддьяковым, заключает ...

Нравственная деятельность педагога
Нравственная деятельность педагога, как и любая духовная деятельность, обладает относительной самостоятельностью, тесно связана с другими видами деятельности и может реализовываться в различных предметных формах: нравственное просвещение, организация нравственного опыта, нравственное самовоспитание ...

Исторические основы активных методов обучения
Под «содержанием образования» понимают типы деятельности, которыми должен овладеть человек, необходимые знания о мире, а также знания о способах получения этих знаний. Существующее сегодня содержание образования ориентировано главным образом на получение сведений, количество которых растет (разбуха ...