Методика преподавания теории вероятностей и математической статистики в средней школе

Нужно дать несколько упражнений на вычисление выражений с факториалами, чтобы учащиеся лучше овладели навыками работы с ними.

Далее рассматривается теорема о выборе с учетом порядка.

Общее количество выбора k элементов из n элементов с учетом порядка определяется формулой 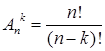и называется числом размещений из n элементов по k элементов.

Приведем пример.

В областных соревнованиях по футболу участвует 8 команд. Требуется определить сколькими способами можно составить группу их 4 команд.

Другими словами, нам нужно выбрать 4 футбольных команды из 8 команд, то есть: .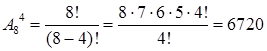

Далее рассматривается теорема о выборе без учета порядка.

Общее количество выборок в схеме выбора k элементов из n без возвращения и без учета порядка определяется формулой 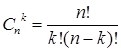и называется числом сочетаний из n элементов по k элементов.

Рассмотрим пример.

На занятии по физкультуре присутствовало 20 человек. Учитель попросил двух человек принести из раздевалки мячи. Сколькими способами можно выбрать учеников, для того чтобы они принесли мячи?

Решение. Порядок в котором будут выбраны ученики не существенен, следовательно: 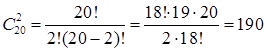способов.

После изучения основных формул комбинаторики следует дать учащимся задачи на вычисление вероятности, для решения которых необходимо применять комбинаторные формулы.

Далее вводим основные операции над событиями. При введении не следует пользоваться кругами Эйлера, так как учащиеся мало знакомы с теорией множеств. После определения операции можно привести пример описывающий данную операцию.

Событие С называется суммой А+В, которое представляет собой событие, состоящее из появлении хотя бы одного из событий А и В.

Бросается кубик. Событие А – выпадет число 2. Событие В – выпадет нечетное число. Тогда событие С=А+В. Будет состоять в выпадении двойки или нечетного числа.

Событие C называется произведением A и B, если оно состоит из всех событий, входящих и в A, и в B.

С=А∙В (А – выпадет 3, В – выпадет нечетное число). Тогда С состоит в выпадении только числа 3, так как 3 является нечетным числом.

Противоположным событию A, называется событие, состоящее в непоявлении события А. Обозначается противоположное событие символом .

Противоположными событиями являются промах и попадание при выстреле, или выпадении герба или цифры при одном подбрасывании монеты.

Далее дадим определения совместных, несовместных событий и зависимых, независимых событий.

События A и B называются несовместными, если они не могут произойти в результате одного испытания. События А и В называются совместными, если они могут произойти в результате одного испытания.

Здесь также следует рассмотреть примеры, для лучшего усвоения этих понятий.

Испытание – один раз подбрасываем монету. События: А – выпадет орел; В – выпадет решка. События А и В несовместны, так как при подбрасывании одной монеты одновременно не выпадет орел и решка.

Событие А называется независимым от события В, если вероятность появления события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Информация по теме:

Гендерные различия восприятия юношами и девушками родительской позиции матери и отца
Исследование тендерных различий восприятия подростками родительской позиции матери и отца представляет особый интерес. Известно, что родительская роль специфицирована в соответствии с полом ребенка, что находит отражение в различных социальных ожиданиях и нормативах поведения, предписываемых общест ...

Метод минимума и максимума
Довольно часто встречаются задачи, в которых требуется определить наибольшее или наименьшее значение величины из всех возможных. Основы такого метода следуют из принципа Ферми, экстремума энергии. В некоторых задачах удается воспользоваться известными алгебраическими неравенствами (Нер-во Коши). За ...

Процес обучения
Под знаниями в обучении понимают основные закономерности предметной области, позволяющие человеку решать конкретные производственные, научные и другие задачи, т.е. факты, понятия, суждения, образы, взаимосвязи, оценки, правила, алгоритмы, эвристики, а также стратегии принятия решений в этой области ...