Методика преподавания теории вероятностей и математической статистики в средней школе

Эту формулу также называют формулой полной вероятности.

Данную формулу можно применить для решения следующей задачи.

Для контроля продукции лыжной фабрики из трех партий лыж взята на проверку одна деталь. Какова вероятность выявления бракованной продукции, если в одной партии 2/3 лыж бракованные, а в двух других все доброкачественные?

Решение. Пусть событие В – взятая деталь бракованная, Ак – деталь берется из к-ой партии, тогда вероятность Р(Ак)=1/3, где к =1; 2; 3.

Пусть в первой партии находятся бракованные лыжи, значит , тогда в двух других партиях нет бракованных лыж, то есть: .

Применяя формулу полной вероятности получим:

.

Для введения формулы Бейеса составим задачу. Пусть дано событие А, оно может наступить при появлении одного из несовместных Событий В1, В2, …, Вn, которые образуют полную группу. Так, как нам заранее не известно, какое событие наступит, их называют гипотезами. Допустим, что произведено испытание в результате, которого появилось событие А. Поставим своей задачей определить, как изменились вероятности гипотез, в связи с тем, что событие А уже наступило. Другими словами определим следующие условные вероятности: , , …, .

Определить данные вероятности можно при помощи формулы Бейеса:

.

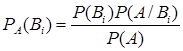Заменив , получим: .

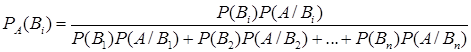Прибор состоит из двух узлов; работа каждого узла необходима для работы прибора в целом. Надежность (вероятность безотказной работы) в течении времени t первого узла равна p1, второго р2. Прибор испытывался в течении времени t, в результате чего обнаружено, что он отказал. Найдите вероятность того, что отказал первый узел, а второй исправен.

Решение. Пусть событие В – прибор отказал, событие А1 – оба узла исправны, А2 – первый узел отказал, а второй испарвен, А3 – первый узел исправен, а второй узел отказал, А4 – оба узла отказали. Эти события образуют полную группу событий. Найдем их вероятности: Р(А1)=р1 р2; Р(А2)=(1-р1)р2; Р(А3)=р1(1-р2);Р(А4)=(1-р1)(1-р2). Так как наблюдалось событие В, то , . Применяя формулу Бейеса получим:

.

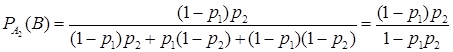Изучение случайных величин требует связи этих величин с определенными событиями, которые заключаются в попадании случайной величины в некоторый интервал и для которых определены вероятности. Другими словами необходимо связать случайную величину с полем данного испытания.

Для лучшего понимания, учителю следует привести пример.

При бросании кости могли появиться цифры 1, 2, 3, 4, 5, 6. Наперед определить число выпавших очков невозможно, так как это зависит от многих случайных величин, которые полностью не могут быть учтены. В этом смысле число очков есть величина случайная; и числа 1, 2, 3, 4, 5, 6 – есть возможные значения этой величины.

Информация по теме:

Диагностика творческих способностей у дошкольников
Гипотеза: Анализ психолого-педагогической литературы позволил нам предположить, что развитие творчества у старших дошкольников в игре возможно, если создаются следующие условия: создание эмоционально-благополучной атмосферы в группе детского сада; гарантия свободы и самостоятельности в игре ребенка ...

Проведение констатирующего эксперимента по изучению сформированности речевых умений детей 2 — 3 летнего возраста
Проведение констатирующего эксперимента, направленного на изучение уровня сформированности речевых умений детей, осуществлялось методом исследования, состоящего из диагностических ситуаций. Блок диагностических ситуаций: «Пассивный взрослый» «Совместная игра со взрослым» «Совместное разглядывание к ...

Методы обучения, их классификация
Понятие «метод обучения» довольно сложное, что обусловлено чрезвычайной многогранностью процесса, который должен отражать сущность данной категории. Г. Ващенко подал содержание общих методов обучения и их классификацию. По его мнению, метод обучения - это средство или система средств, сознательно п ...